Machine Learning

A Gentle Introduction

Sakeef M. Karim
New York University


CONSORTIUM ON ANALYTICS FOR DATA-DRIVEN DECISION-MAKING

Roadmap

What We’ll Cover Today

  • What machine learning (ML) means in substantive terms

  • How machine learning differs from classical social statistics

    • The two cultures?

  • Key terms and concepts

    • Bias-Variance Tradeoff
    • Training, Validation and Testing
    • \(k\)-Fold Cross-Validation
    • Hyperparameter Optimization

  • An introduction to \(k\)-Nearest Neighbours algorithms

What is Machine Learning?

Defining Machine Learning

  • A broad definition

    • A branch of artificial intelligence (AI) that involves using algorithms and statistical models to enable computer systems to automatically learn from data (via ChatGPT).

  • A more concrete definition

  • An even more concrete definition

    • A way to learn from data and estimate complex functions that discover representations of some input (\(X\)), or link the input to an output (\(Y\)) in order to make predictions on new data (see Molina and Garip 2019).

Supervised Machine Learning (SML)

  • Once deployed, SML algorithms learn the complex patterns linking \(X\)—a set of features (or independent variables)—to a target variable (or outcome), \(Y\).

    • The goal of SML is to optimize predictions—i.e., to find functions or algorithms that offer substantial predictive power when confronted with new or unseen data.

    • Examples of SML algorithms include logistic regressions, random forests, ridge regressions and neural networks.

  • A quick note on terminology

    • If a target variable is quantitative, we are dealing with a regression problem.

    • If a target variable is qualitative, we are dealing with a classification problem.

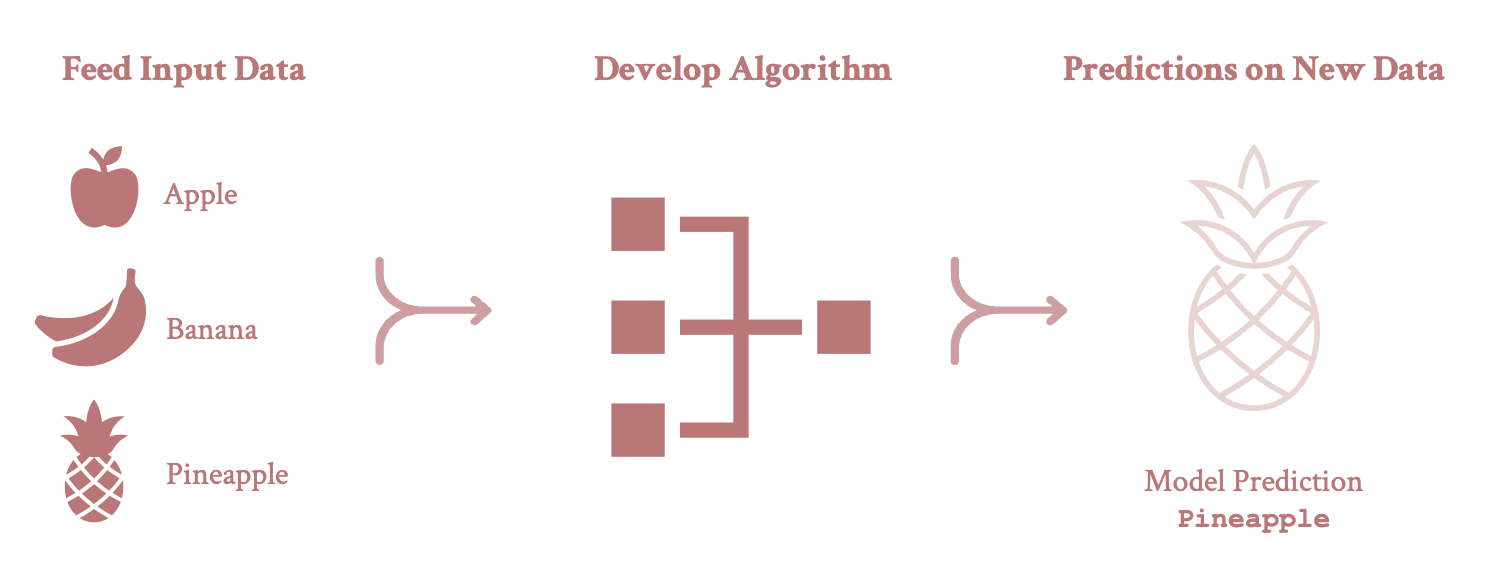
Note: This figure is an adaptation of the diagram depicted here

Unsupervised Machine Learning (UML)

  • UML techniques search for a representation of the inputs (or features) that is more useful than \(X\) itself (Molina and Garip 2019).

    • Put another way, UML algorithms search for hidden structure in high dimensional space.

  • In UML, there is no observed \(Y\) variable—or target—to supervise the estimation process. Instead, we only have a vector of inputs to work with.

  • The goal in UML is to develop a lower-dimensional representation of complex data by inductively learning from the interrelationships among inputs.

    • This can be achieved by reducing a vector of features to a smaller set of scales (e.g., via principal component analysis) or partitioning the sample into a small number of unobserved groups (e.g., via k-means clustering).

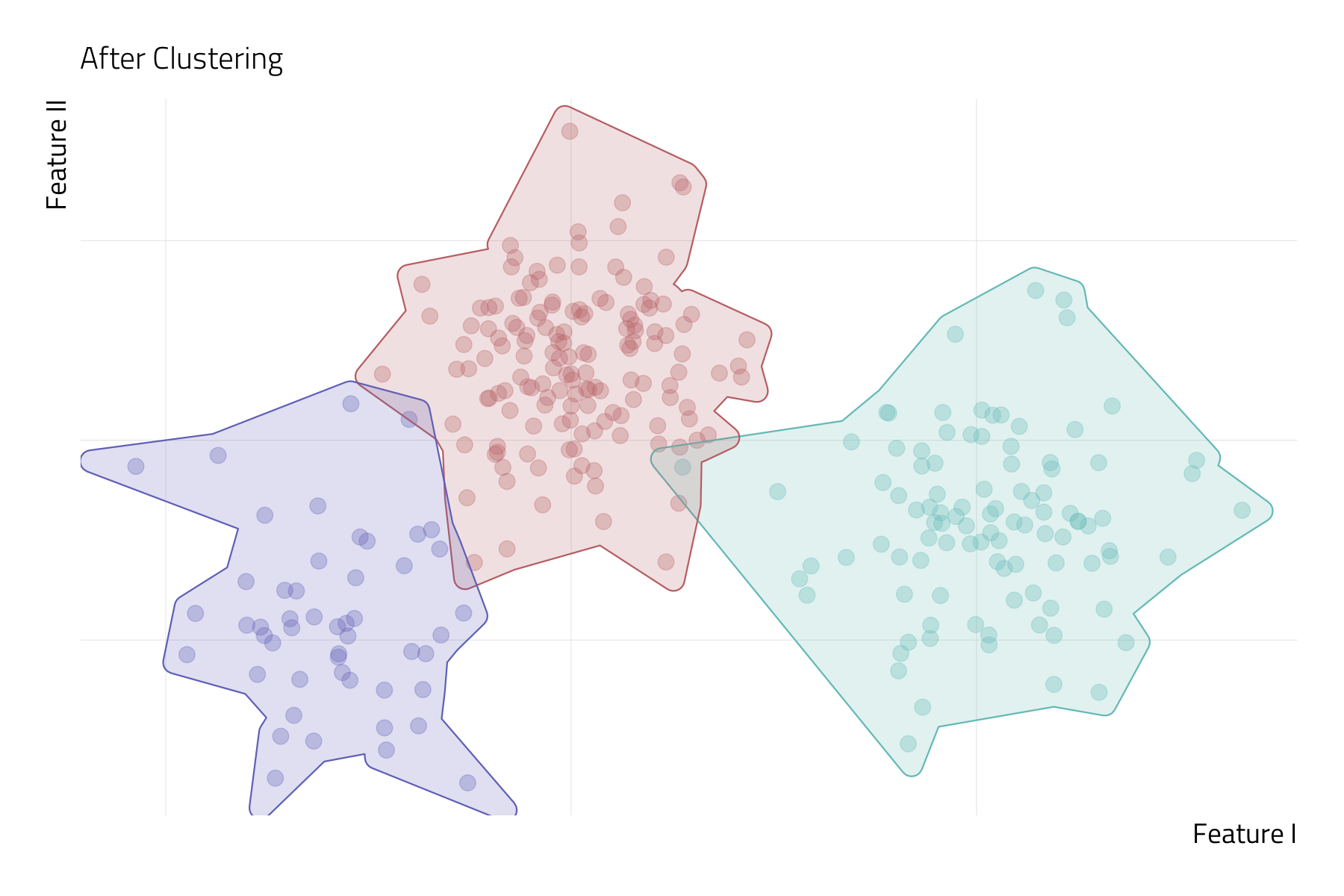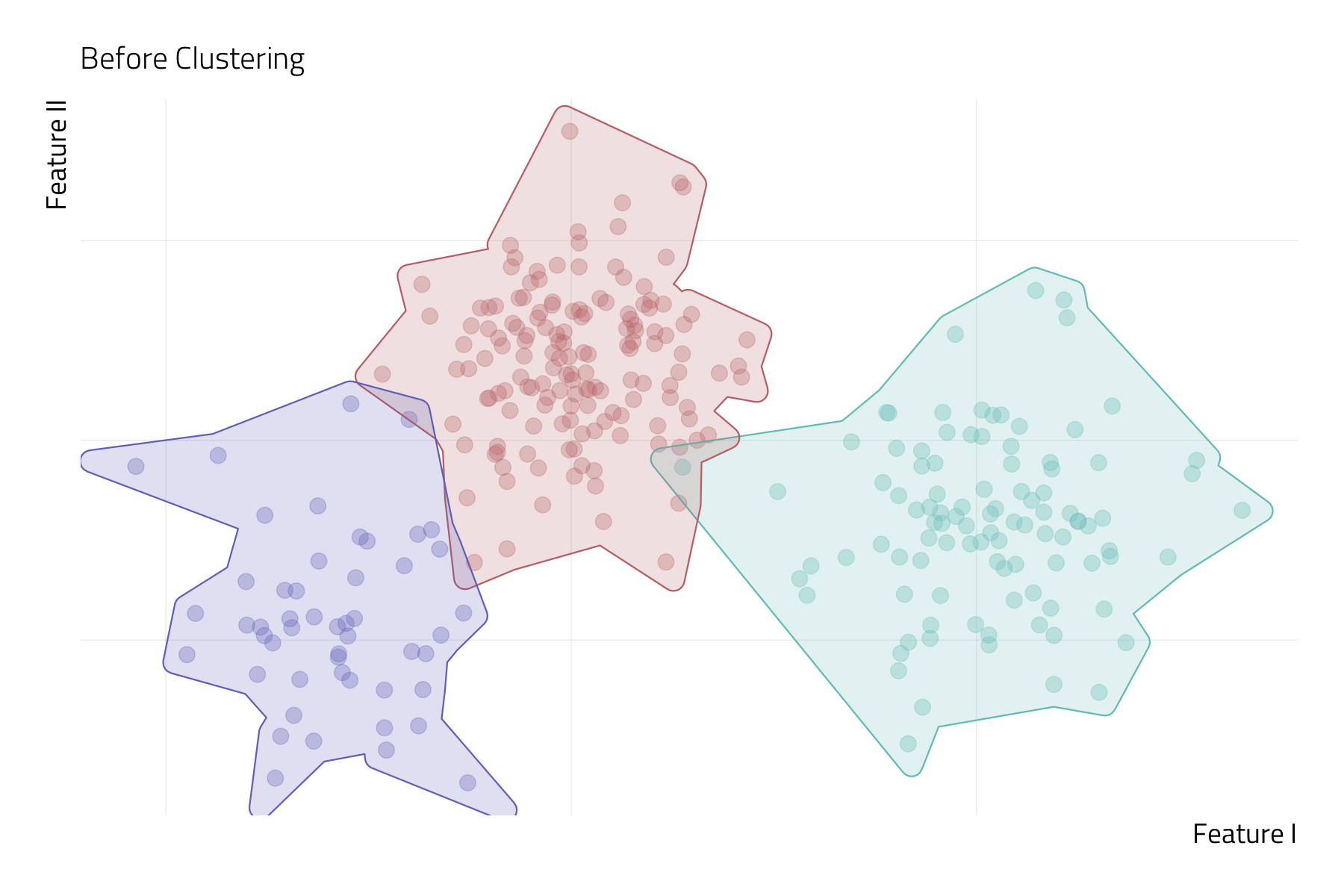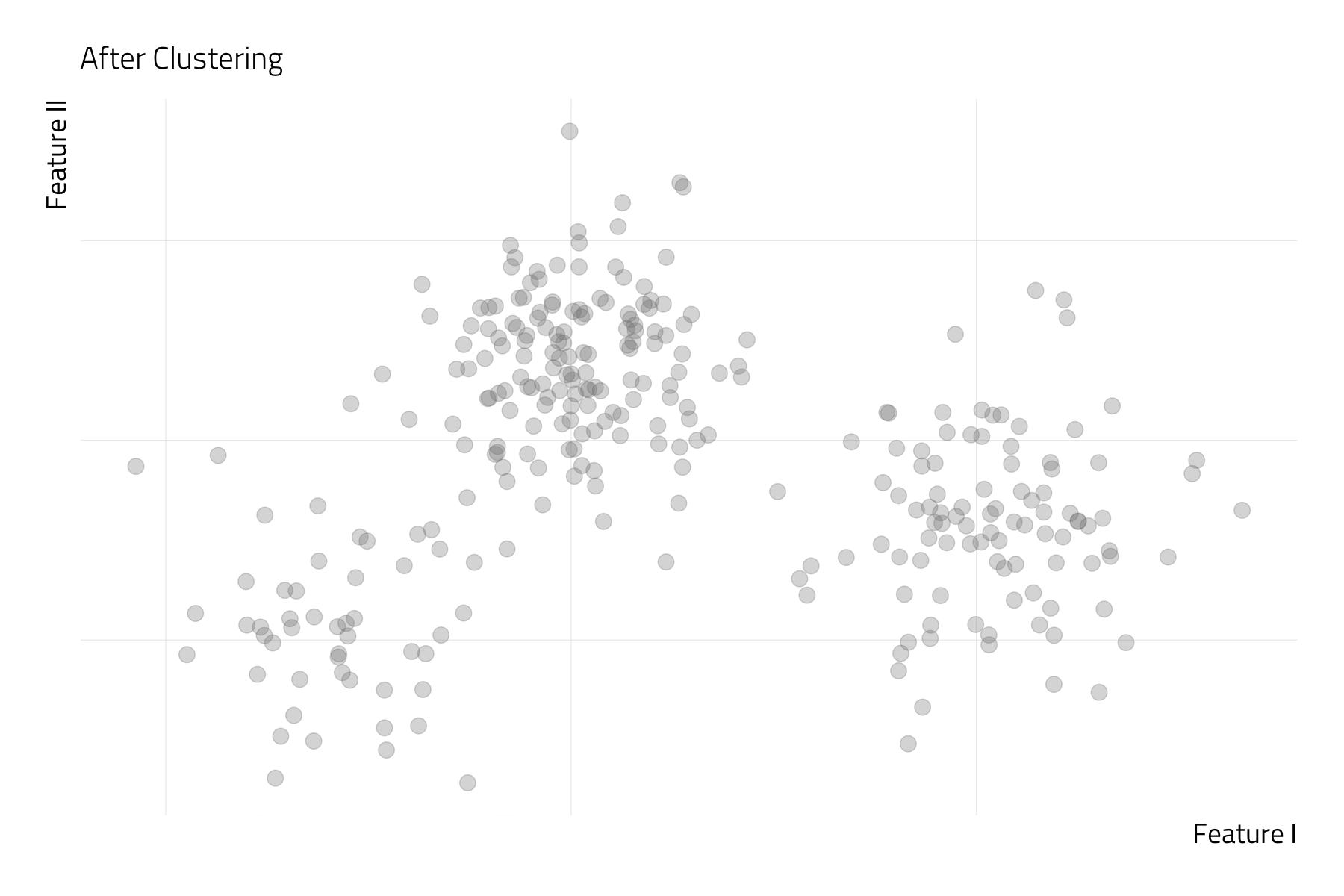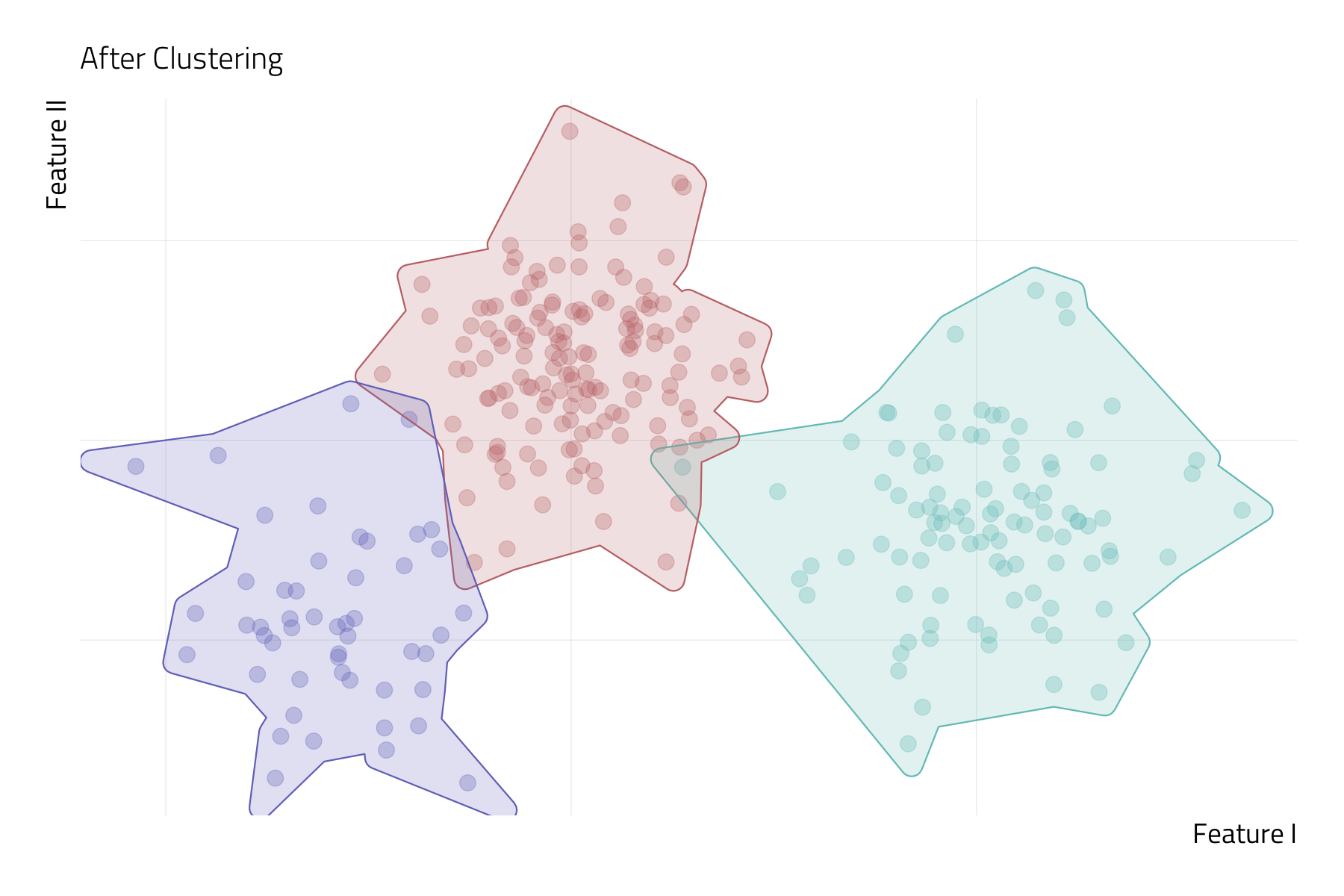
Machine Learning vs Classical Statistics

The Two Cultures

  • As Grimmer and colleagues (2021) note, “machine learning is as much a culture defined by a distinct set of values and tools as it is a set of algorithms.”

  • This point has, of course, been made elsewhere.

    • Breiman (2001) famously used the imagery of warring cultures to describe two major traditions—(i) the generative modelling culture and (ii) the predictive modelling culture—that have achieved hegemony within the world of statistical modelling.

    • The terms generative and predictive (as opposed to data and algorithmic) come from Donoho’s (2017) 50 Years of Data Science.

The Two Cultures (cont.)


Quantity of Interest Primary Goals Key Strengths Key Limitations
Generative (i.e., Classical Statistics)

Inferring relationships between X and Y

Interpretability; emphasis on uncertainty around estimates; explanatory power

Bounded by statistical assumptions, inattention to variance across samples

Predictive (i.e., Machine Learning)

Generating accurate predictions of Y

Predictive power; potential to simplify high dimensional data; relatively unconstrained by statistical assumptions

Inattention to explanatory processes, opaque links between X and Y

Note: To be sure, the putative strengths and weaknesses of these modelling “cultures” have been hotly debated.

The Affordances of Machine Learning

  • Advances in machine learning can provide empirical leverage to social scientists and sharpen social theory in one fell swoop.

  • Lundberg, Brand and Jeon (2022), for instance, argue that adopting a machine learning framework can help social scientists:

    • Amplify human coding
    • Summarize complex data structures
    • Relax statistical assumptions
    • Target researcher attention

  • While ML is often associated with induction, van Loon (2022) argues that SML algorithms can help us deductively resolve predictability hypotheses as well.

    • What plays a larger role in shaping human behaviour—nature or nurture?

Key Terms and Concepts in the SML Setting

Bias-Variance Tradeoff

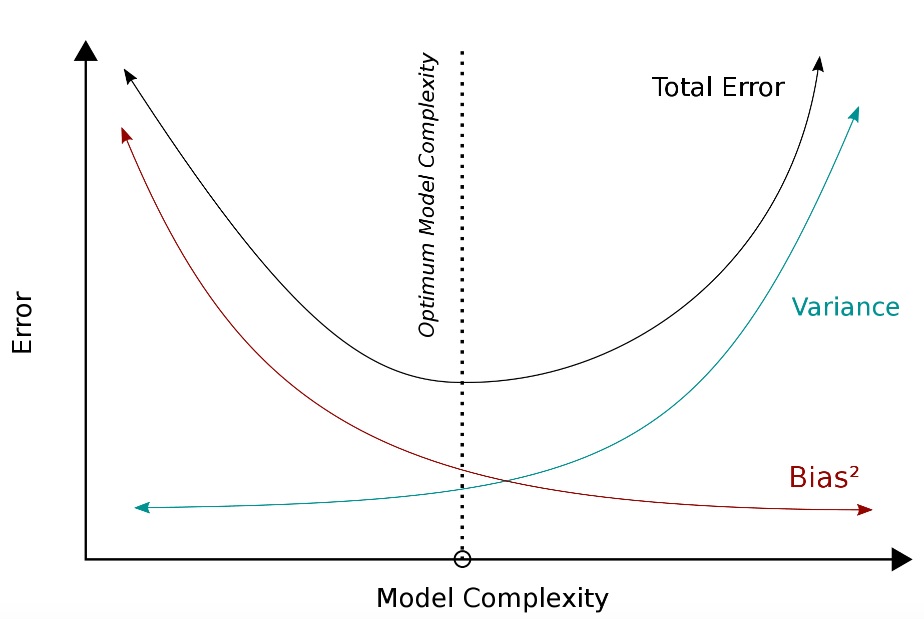
Image can be retrieved here.

  • Bias emerges when we build SML algorithms that fail to sufficiently map the patterns—or pick up the empirical signal–linking \(X\) and \(Y\). Think: underfitting.

  • Variance arises when our algorithms not only pick up the signal linking \(X\) and \(Y\), but some of the noise in our data as well. Think: overfitting.

  • When adopting an SML framework, researchers try to strike the optimal balance between bias and variance.

Training, Validation and Testing

  • In an SML setting, we want to reduce our algorithm’s generalization or test error—i.e., “the prediction error of a model on new data” (Molina and Garip 2019).
  • To arrive at an estimate of our model’s performance, we can (randomly) partition our global sample of observations into disjoint sets or subsamples.

  • We can use a training set to fit our algorithm—to find weights (or coefficients), recursively split the feature space to grow decision trees and so on.

  • Training data should constitute the largest of our three disjoint sets.

  • We can use a validation set to find the right estimator out of a series of candidate algorithms—or to choose the best-fitting parameterization of a single algorithm.

  • Often, using both training and validation sets can be costly: data sparsity can give rise to bias.

  • Thus, when limited to smaller samples, analysts often combine training and validation—say, by recycling training data for model tuning and selection.

  • We can use a testing set to generate a measure of our model’s predictive accuracy (e.g., the F1 score for classification problems)—or to derive our generalization error.

  • This subsample is used only once (to report the performance metric); put another way, it cannot be used to train, tune or select our algorithm.

\(k\)-Fold Cross-Validation

  • Unlike conventional approaches to sample partition, \(k\) or \(v\)-fold cross-validation allows us to learn from all our data.

  • \(k\)-fold cross-validation proceeds as follows:

    • We randomly divide our overall sample into \(k\) subsets or folds.
    • We train our algorithm on \(k - 1\) folds, holding just one group out for model assessment.
    • We repeat this process \(k\) times—every fold is held out once and used to fit the model \(k - 1\) times.
    • We then pool or average the evaluation metrics (e.g., predictive accuracy) for all the held-out runs.

  • Stratified \(k\)-fold cross-validation ensures that the distribution of class labels (or for numeric targets, the mean) is relatively constant across folds.











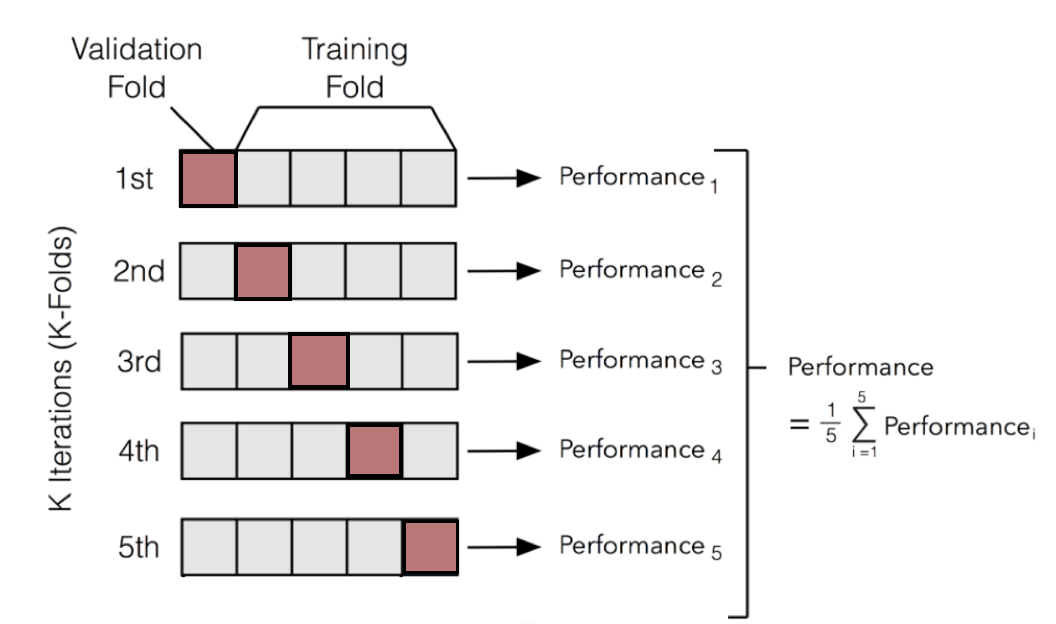
Image can be retrieved here.

Hyperparameter Optimization

  • In SML settings, we automatically learn the parameters (e.g., coefficients) of our algorithms during estimation.

  • Hyperparameters, on the other hand, are chosen by the analyst, guide the entire learning process, and can powerfully shape our algorithm’s predictive performance.

    • Examples of hyperparameters include the \(k\) in nearest neighbours algorithms, the \(\alpha\) penalty term in ridge regressions, or the number of hidden layers in a neural network.

  • How can analysts settle on the right hyperparameter value(s) for their algorithm?

    • Test different values via trial and error.
    • Use automated procedures like GridSearchCV from scikit-learn.

\(k\)-Nearest Neighbours

Brief Overview of KNN

  • \(k\)-nearest neighbours (KNNs) are simple, non-parametric algorithms that predict values of \(Y\) based on the distance between rows (or observations’ inputs).

  • The estimation of KNNs proceeds as follows:

    • The analyst defines the distance metric (e.g., Euclidean, Manhattan) they will use to determine how similar any two observations are based on their vector of features.
    • The analyst defines a value for the hyperparameter \(k\)—that is, the number of nearest neighbours to find in the training subsample.
    • When fed a new data point, KNNs find the \(k\) nearest neighbours in the training data, and:
      • Assign the new observation to the class that most of its \(k\) nearest neighbours belong to (for classification problems.)
      • Generate a prediction of \(Y\) by taking the average of the target variable for the new observation’s \(k\) nearest neighbours (for regression problems.)

KNN in Python

Initial Steps 
# Importing pandas to wrangle the data, modules from scikit-learn to fit KNN classifier,
# and numpy to iterate over potential values of k (for a grid search):

import pandas as pd 

from sklearn.neighbors import KNeighborsClassifier

from sklearn.model_selection import train_test_split, cross_val_score, StratifiedKFold, GridSearchCV

import numpy as np

# Load input data frame:

data = pd.read_csv("https://gattonweb.uky.edu/sheather/book/docs/datasets/MichelinNY.csv", 
                   encoding ='latin-1')
                   
# Zero-in on X and Y variables:

y = data['InMichelin']

X = data.drop(columns = ['InMichelin', 'Restaurant Name'])
Performing Train-Test Split, Estimating First Model (\(k\) = 5) 
# Perform train-test split:

X_train, X_test, y_train, y_test = train_test_split(X, y, stratify = y, test_size = 0.2, random_state = 905)
                                                    
# Initializing KNN classifier with k = 5, fitting model:

knn = KNeighborsClassifier(n_neighbors = 5)

knn.fit(X_train.values, y_train)

# Stratified k-fold cross-validation:

skfold = StratifiedKFold(n_splits = 10, shuffle = True, random_state = 905)

# Cross-validation score:

cross_val_score(knn, X_train, y_train, cv = skfold).mean()

# Measure of predictive performance:

knn.score(X_test.values, y_test)
Finding An Optimal Value of \(k\) 
# Creating a grid of potential hyperparameter values (odd numbers from 1 to 13):

k_grid = {'n_neighbors': np.arange(start = 1, stop = 15, step = 2) }

# Setting up a grid search to home-in on best value of k:

grid = GridSearchCV(KNeighborsClassifier(), param_grid = k_grid, cv = skfold)

grid.fit(X_train, y_train)

# Extract best score and hyperparameter value:

print("Best Mean Cross-Validation Score: {:.3f}".format(grid.best_score_))

print("Best Parameters (Value of k): {}".format(grid.best_params_))

print("Test Set Score: {:.3f}".format(grid.score(X_test, y_test)))

A Quick Exercise

Using data from {palmerpenguins}, develop a \(k\)-nearest neighbours regressor or classifier to predict an outcome of interest. Try to report your algorithm’s cross-validation score and out-of-sample performance.

If you don’t remember how to work with the {palmerpenguins} package in Python, return to the Jupyter Notebook hyperlinked here.

The End (for now)

References

Breiman, Leo. 2001. “Statistical Modeling: The Two Cultures (with Comments and a Rejoinder by the Author).” Statistical Science 16 (3). https://doi.org/10.1214/ss/1009213726.
Donoho, David. 2017. “50 Years of Data Science.” Journal of Computational and Graphical Statistics 26 (4): 745–66. https://doi.org/10.1080/10618600.2017.1384734.
Grimmer, Justin, Margaret E. Roberts, and Brandon M. Stewart. 2021. “Machine Learning for Social Science: An Agnostic Approach.” Annual Review of Political Science 24 (1): 395–419. https://doi.org/10.1146/annurev-polisci-053119-015921.
Lundberg, Ian, Jennie E. Brand, and Nanum Jeon. 2022. “Researcher Reasoning Meets Computational Capacity: Machine Learning for Social Science.” Social Science Research 108 (November): 102807. https://doi.org/10.1016/j.ssresearch.2022.102807.
Molina, Mario, and Filiz Garip. 2019. “Machine Learning for Sociology.” Annual Review of Sociology 45 (1): 27–45. https://doi.org/10.1146/annurev-soc-073117-041106.
van Loon, Austin. 2022. “Machine Learning and Deductive Social Science: An Introduction to Predictability Hypotheses.” SocArXiv. https://doi.org/10.31235/osf.io/s7uer.